This specification defines asm.js, a strict subset of JavaScript that can be used as a low-level, efficient target language for compilers. This sublanguage effectively describes a sandboxed virtual machine for memory-unsafe languages like C or C++. A combination of static and dynamic validation allows JavaScript engines to employ an ahead-of-time (AOT) optimizing compilation strategy for valid asm.js code.
This specification is working towards a candidate draft for asm.js version 1. Mozilla's SpiderMonkey JavaScript engine provides an optimizing implementation of this draft.
case and default validation rules
mut
doublish to double? for symmetry with float?
Math.fround and singleton fround type
float support for operators and Math functions
float to legal result types for ConditionalExpression
Math.min and Math.max
Math.abs is signed
unsigned is not an extern type
! operator to UnaryExpression operators
~~ to Unary Operators section
-NumericLiteral cases everywhere
unknown, which is no longer needed
% is intish
This specification defines asm.js, a strict subset of JavaScript that can be used as a low-level, efficient target language for compilers. The asm.js language provides an abstraction similar to the C/C++ virtual machine: a large binary heap with efficient loads and stores, integer and floating-point arithmetic, first-order function definitions, and function pointers.
The asm.js programming model is built around integer and floating-point arithmetic and a virtual heap represented as a typed array. While JavaScript does not directly provide constructs for dealing with integers, they can be emulated using two tricks:
As an example of the former, if we have
an Int32Array
view of the heap called HEAP32, then we can load the
32-bit integer at byte offset p:
HEAP32[p >> 2]|0
The shift converts the byte offset to a 32-bit element offset, and
the bitwise coercion ensures that an out-of-bounds access is coerced
from undefined back to an integer.
As an example of integer arithmetic, addition can be performed by taking two integer values, adding them with the built-in addition operator, and coercing the result back to an integer via the bitwise or operator:
(x+y)|0
This programming model is directly inspired by the techniques pioneered by the Emscripten and Mandreel compilers.
The asm.js sub-language is defined by a static type system that can be checked at JavaScript parse time. Validation of asm.js code is designed to be "pay-as-you-go" in that it is never performed on code that does not request it. An asm.js module requests validation by means of a special prologue directive, similar to that of ECMAScript Edition 5's strict mode:
function MyAsmModule() {
"use asm";
// module body
}
This explicit directive allows JavaScript engines to avoid performing pointless and potentially costly validation on other JavaScript code, and to report validation errors in developer consoles only where relevant.
Because asm.js is a strict subset of JavaScript, this specification only defines the validation logic—the execution semantics is simply that of JavaScript. However, validated asm.js is amenable to ahead-of-time (AOT) compilation. Moreover, the code generated by an AOT compiler can be quite efficient, featuring:
Code that fails to validate must fall back to execution by traditional means, e.g., interpretation and/or just-in-time (JIT) compilation.
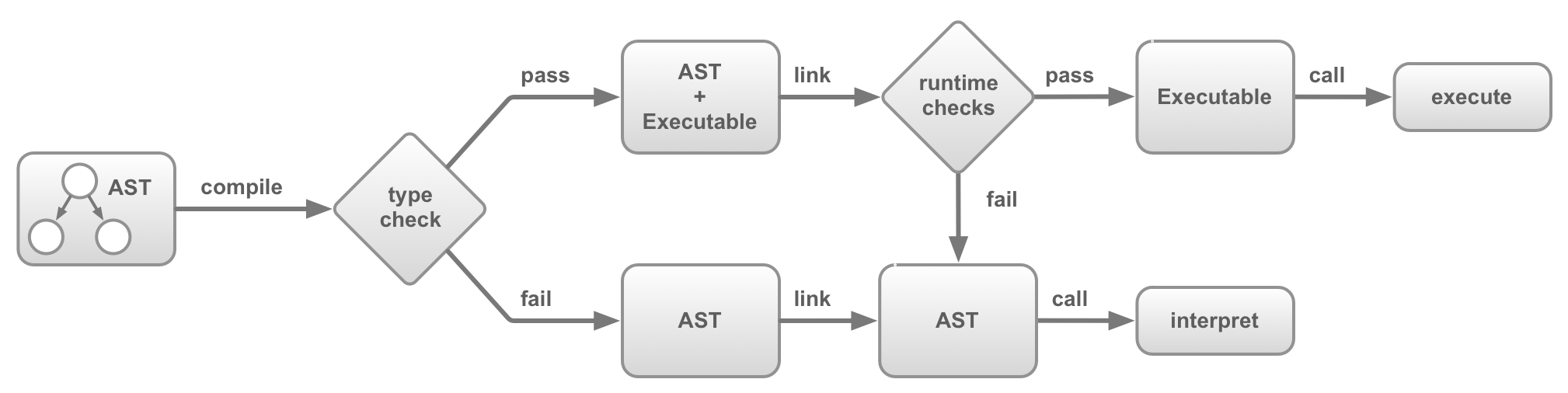
Using an asm.js module requires calling its function to obtain an object containing the module's exports; this is known as linking. An asm.js module can also be given access to standard libraries and custom JavaScript functions through linking. An AOT implementation must perform certain dynamic checks to check compile-time assumptions about the linked libraries in order to make use of the compiled code.
This figure depicts a simple architecture of an AOT implementation that otherwise employs a simple interpreter. If either dynamic or static validation fails, the implementation must fall back to the interpreter. But if both validations succeed, calling the module exports executes the binary executable code generated by AOT compilation.

Within an asm.js module, all code is fully statically typed and limited to the very restrictive asm.js dialect. However, it is possible to interact with recognized standard JavaScript libraries and even custom dynamic JavaScript functions.
An asm.js module can take up to three optional parameters, providing access to external JavaScript code and data:
ArrayBuffer
to act as the asm.js heap.
These objects allow asm.js to call into external JavaScript (and to share its heap buffer with external JavaScript). Conversely, the exports object returned from the module allows external JavaScript to call into asm.js.
So in the general case, an asm.js module declaration looks like:
function MyAsmModule(stdlib, foreign, heap) {
"use asm";
// module body...
return {
export1: f1,
export2: f2,
// ...
};
}
Function parameters in asm.js are provided a type annotation by means of an explicit coercion on function entry:
function geometricMean(start, end) {
start = start|0; // start has type int
end = end|0; // end has type int
return +exp(+logSum(start, end) / +((end - start)|0));
}
These annotations serve two purposes: first, to provide the function's type signature so that the validator can enforce that all calls to the function are well-typed; second, to ensure that even if the function is exported and called by external JavaScript, its arguments are dynamically coerced to the expected type. This ensures that an AOT implementation can use unboxed value representations, knowing that once the dynamic coercions have completed, the function body never needs any runtime type checks.
The following is a small but complete example of an asm.js module.
function GeometricMean(stdlib, foreign, buffer) {
"use asm";
var exp = stdlib.Math.exp;
var log = stdlib.Math.log;
var values = new stdlib.Float64Array(buffer);
function logSum(start, end) {
start = start|0;
end = end|0;
var sum = 0.0, p = 0, q = 0;
// asm.js forces byte addressing of the heap by requiring shifting by 3
for (p = start << 3, q = end << 3; (p|0) < (q|0); p = (p + 8)|0) {
sum = sum + +log(values[p>>3]);
}
return +sum;
}
function geometricMean(start, end) {
start = start|0;
end = end|0;
return +exp(+logSum(start, end) / +((end - start)|0));
}
return { geometricMean: geometricMean };
}
In a JavaScript engine that supports AOT compilation of asm.js, calling the module on a proper global object and heap buffer would link the exports object to use the statically compiled functions.
var heap = new ArrayBuffer(0x10000); // 64k heap init(heap, START, END); // fill a region with input values var fast = GeometricMean(window, null, heap); // produce exports object linked to AOT-compiled code fast.geometricMean(START, END); // computes geometric mean of input values
By contrast, calling the module on a standard library object
containing something other than the true Math.exp or
Math.log would fail to produce AOT-compiled code:
var bogusGlobal = {
Math: {
exp: function(x) { return x; },
log: function(x) { return x; }
},
Float64Array: Float64Array
};
var slow = GeometricMean(bogusGlobal, null, heap); // produces purely-interpreted/JITted version
console.log(slow.geometricMean(START, END)); // computes bizarro-geometric mean thanks to bogusGlobal
Validation of an asm.js module relies on a static type system that classifies and constrains the syntax. This section defines the types used by the validation logic.
Validation in asm.js limits JavaScript programs to only use operations that can be mapped closely to efficient data representations and machine operations of modern architectures, such as 32-bit integers and integer arithmetic.
The types of asm.js values are inter-related by a subtyping relation, which can be represented pictorially:
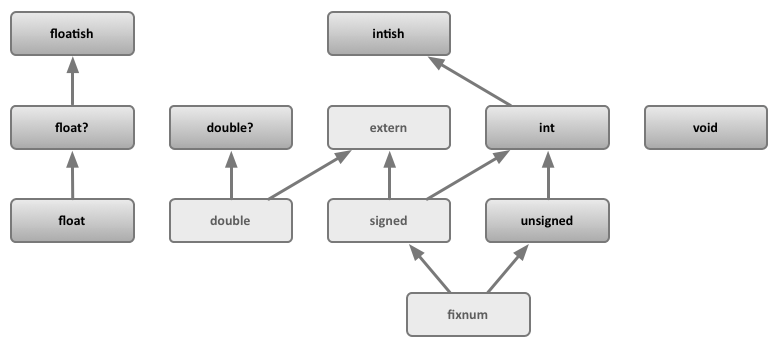
The light boxes represent arbitrary JavaScript values that may flow freely between asm.js code and external JavaScript code.
The dark boxes represent types that are disallowed from escaping into external (i.e., non-asm.js) JavaScript code. (These values can be given efficient, unboxed representations in optimized asm.js implementations that would be unsound if they were allowed to escape.)
The meta-variables σ and τ are used to stand for value types.
The void type is the type of functions that
are not supposed to return any useful value. As JavaScript functions,
they produce the undefined value, but asm.js code is not
allowed to make use of this value; functions with return
type void can only be called for effect.
The double type is the type of ordinary
JavaScript double-precision floating-point numbers.
The signed type is the type of signed
32-bit integers. While there is no direct concept of integers in
JavaScript, 32-bit integers can be represented as doubles, and integer
operations can be performed with JavaScript arithmetic, relational,
and bitwise operators.
The unsigned type is the type of unsigned
32-bit integers. Again, these are not a first-class concept in
JavaScript, but can be represented as floating-point numbers.
The int type is the type of 32-bit integers
where the signedness is not known. In asm.js, the type of a variable
never has a known signedness. This allows them to be compiled as
32-bit integer registers and memory words. However, this
representation creates an overlap between signed and unsigned numbers
that causes an ambiguity in determining which JavaScript number they
represent. For example, the bit pattern 0xffffffff could
represent 4294967295 or -1, depending on the signedness. For this
reason, values of the int type are disallowed from
escaping into external (non-asm.js) JavaScript code.
The fixnum type is the type of integers in the
range [0, 231)—that is, the range of integers such
that an unboxed 32-bit representation has the same value whether it is
interpreted as signed or unsigned.
Even though JavaScript only supports floating-point arithmetic, most operations can simulate integer arithmetic by coercing their result to an integer. For example, adding two integers may overflow beyond the 32-bit range, but coercing the result back to an integer produces the same 32-bit integer as integer addition in, say, C.
The intish type represents the result of a
JavaScript integer operation that must be coerced back to an integer
with an explicit coercion
(ToInt32
for signed integers
and ToUint32
for unsigned integers). Validation requires all intish
values to be immediately passed to an operator or standard library
that performs the appropriate coercion or else dropped via an
expression statement. This way, each integer operation can be
compiled directly to machine operations.
The one operator that does not support this approach is
multiplication. (Multiplying two large integers can result in a large
enough double that some lower bits of precision are lost.) So asm.js
does not support applying the multiplication operator to integer
operands. Instead, the
proposed Math.imul
function is recommended as the proper means of implementing integer
multiplication.
The double? type represents operations that
are expected to produce a double but may also produce
undefined, and so must be coerced back to a number
via ToNumber.
Specifically, reading out of bounds from a typed array
produces undefined.
The float type is the type of 32-bit
floating-point numbers.
The float? type represents operations that
are expected to produce a float but, similar
to double?, may also produce undefined and
so must be coerced back to a 32-bit floating point number
via fround.
Specifically, reading out of bounds from a typed array
produces undefined.
Similar to integers, JavaScript can almost support 32-bit floating-point arithmetic, but requires extra coercions to properly emulate the 32-bit semantics. As proved in When is double rounding innocuous? (Figueroa 1995), both the 32- and 64-bit versions of standard arithmetic operations produce equivalent results when given 32-bit inputs and coerced to 32-bit outputs.
The floatish type,
like intish, represents the result of a JavaScript 32-bit
floating-point operations that must be coerced back to a 32-bit
floating-point value with an
explicit fround
coercion. Validation requires all floatish values to be
immediately passed to an operator or standard library that performs
the appropriate coercion or else dropped via an expression
statement. This way, each 32-bit floating-point operation can be
compiled
directly to machine operations.
extern type represents the root
of all types that can escape back into external JavaScript—in
other words, the light boxes in the above diagram.
Variables and functions defined at the top-level scope of an asm.js module can have additional types beyond the value types. These include:
ArrayBufferView types IntnArray, UintnArray, and FloatnArray;
…) → τ) ∧ … ∧ ((σ′, σ′…) → τ′);
fround of Math.fround; and
Function.
The "∧" notation for function types serves to represent
overloaded functions and operators. For example,
the Math.abs function is
overloaded to accept either integers or floating-point numbers, and
returns a different type in each case. Similarly, many of
the operators have overloaded types.
The meta-variable γ is used to stand for global types.
Validating an asm.js module depends on tracking contextual information about the set of definitions and variables in scope. This section defines the environments used by the validation logic.
An asm.js module is validated in the context of a global environment. The global environment maps each global variable to its type as well as indicating whether the variable is mutable:
The meta-variable Δ is used to stand for a global environment.
In addition to the global environment, each function body in an asm.js module is validated in the context of a variable environment. The variable environment maps each function parameter and local variable to its value type:
{ x : τ, … }
The meta-variable Γ is used to stand for a variable environment.
Looking up a variable's type
is defined by:
mut γ or x : imm γ
occurs in Δ
If x does not occur in either environment then the Lookup function has no result.
Validation of an asm.js module is specified by reference to the ECMAScript grammar, but conceptually operates at the level of abstract syntax. In particular, an asm.js validator must obey the following rules:
;) are always ignored, whether in
the top level of a module or inside an asm.js function body.
eval
or arguments.
These rules are otherwise left implicit in the rest of the specification.
All variables in asm.js are explicitly annotated with type information so that their type can be statically enforced by validation.
Every parameter in an asm.js function is provided with an explicit
type annotation in the form of a coercion. This coercion serves two
purposes: the first is to make the parameter type statically apparent
for validation; the second is to ensure that if the function is
exported, the arguments dynamically provided by external JavaScript
callers are coerced to the expected type. For example, a bitwise OR
coercion annotates a parameter as having type int:
function add1(x) {
x = x|0; // x : int
return (x+1)|0;
}
In an AOT implementation, the body of the function can be
implemented fully optimized, and the function can be given two entry
points: an internal entry point for asm.js callers, which are
statically known to provide the proper type, and an external dynamic
entry point for JavaScript callers, which must perform the full
coercions (which might involve arbitrary JavaScript computation, e.g.,
via implicit calls to valueOf).
There are three recognized parameter type annotations:
= x:Identifier|0;= +x:Identifier;= f:Identifier(x:Identifier);
The first form annotates a parameter as type int, the
second as type double, and the third as
type float. In the latter case,
Lookup(Δ, Γ, f) must
be fround.
An asm.js function's formal return type is determined by
the last statement in the function body, which for
non-void functions is required to be
a ReturnStatement. This distinguished return statement may
take one of five forms:
return +e:Expression;return e:Expression|0;return n:-NumericLiteral;return f:Identifier(arg:Expression);return;
The first form has return type double. The second has
type signed. The third has return
type double if n is composed of a floating-point
literal, i.e., a numeric literal with the character . in
its source; alternatively, if n is composed of an integer
literal and has its value in the range [-231,
231), the return statement has return
type signed. The fourth form has return
type float, and the fifth has return
type void.
If the last statement in the function body is not
a ReturnStatement, or if the function body has no non-empty
statements (other than the initial declarations and
coercions—see Function
Declarations), the function's return type is void.
The type of a function declaration
function f:Identifier(x:Identifier…) { x:Identifier = AssignmentExpression;… var y:Identifier = -NumericLiteral Identifier(-NumericLiteral),…… body:Statement…}
is (σ,…) → τ where σ,… are the
types of the parameters, as provided by
the parameter type
annotations, and τ is the formal return type, as provided by
the return type annotation. The
variable f is stored in
the global environment with
type imm (σ,…) → τ.
The types of variable declarations are determined by their initializer, which may take one of two forms:
-NumericLiteral(n:-NumericLiteral)
In the first case, the variable type is double
if n's source contains the character .;
otherwise n may be an integer literal in the range
[-231, 232), in which case the variable type
is int.
In the second case, the variable type
is float. Lookup(Δ, Γ, f)
must be fround and n must be a floating-point
literal with the character . in its source.
A global variable declaration is a VariableStatement node in one of several allowed forms. Validating global variable annotations takes a Δ as input and produces as output a new Δ′ by adding the variable binding to Δ.
A global program variable is initialized to a literal:
var x:Identifier = n:-NumericLiteral;var x:Identifier = f:Identifier(n:-NumericLiteral);
The global variable x is stored in
the global environment with
type mut τ, where τ is determined in the same way
as local variable type
annotations.
A standard library import is of one of the following two forms:
var x:Identifier = stdlib:Identifier.y:Identifier;var x:Identifier = stdlib:Identifier.Math.y:Identifier;
The variable stdlib must match the first parameter of
the module declaration. The global
variable x is stored in
the global environment with
type imm γ, where γ is the type of
library y or Math.y as specified by
the standard library types.
A foreign import is of one of the following three forms:
var x:Identifier = foreign:Identifier.y:Identifier;var x:Identifier = foreign:Identifier.y:Identifier|0;var x:Identifier = +foreign:Identifier.y:Identifier;
The variable foreign must match the second parameter of
the module declaration. The global
variable x is stored in
the global environment with
type imm Function for the first form, mut
int for the second, and mut double for the third.
A global heap view is of the following form:
var x:Identifier = new stdlib:Identifier.view:Identifier(heap:Identifier);
The variable stdlib must match the first parameter of
the module declaration and the
variable heap must match the third. The
identifier view must be one of the
standard ArrayBufferView
type names. The global variable x is stored in
the global environment with
type imm
view.
A function table is a VariableStatement of the form:
var x:Identifier = [f0:Identifier, f:Identifier,…];
The function table x is stored in
the global environment with
type imm ((σ,…) → τ)[n]
where (σ,…) → τ is the type of f in the
global environment and n is the length of the array literal.
To ensure that a JavaScript function is a proper asm.js module, it must first be statically validated. This section specifies the validation rules. The rules operate on JavaScript abstract syntax, i.e., the output of a JavaScript parser. The non-terminals refer to parse nodes defined by productions in the ECMAScript grammar, but note that the asm.js validator only accepts a subset of legal JavaScript programs.
The result of a validation operation is either a success, indicating that a parse node is statically valid asm.js, or a failure, indicating that the parse node is statically invalid asm.js.
The ValidateModule rule validates an asm.js module, which is either a FunctionDeclaration or FunctionExpression node.
Validating a module of the form
function f:Identifieropt(stdlib:Identifier, foreign:Identifier, heap:Identifieroptoptopt) {
"use asm"; var:VariableStatement… fun:FunctionDeclaration… table:VariableStatement… exports:ReturnStatement}
succeeds if:
The ValidateExport rule validates an asm.js module's export declaration. An export declaration is a ReturnStatement returning either a single asm.js function or an object literal exporting multiple asm.js functions.
Validating an export declaration node
return { x:Identifier : f:Identifier,… };
succeeds if for each f, Δ(f) = imm
γ where γ is a function type (σ,…) →
τ.
Validating an export declaration node
return f:Identifier;
succeeds if Δ(f) = imm γ where
γ is a function type (σ,…) → τ.
The ValidateFunctionTable rule validates an asm.js module's function table declaration. A function table declaration is a VariableStatement binding an identifier to an array literal.
Validating a function table of the form
var x:Identifier = [f:Identifier,…];
succeeds if:
imm ((σ,…) → τ)[n]; and
The ValidateFunction rule validates an asm.js function declaration, which is a FunctionDeclaration node.
Validating a function declaration of the form
function f:Identifier(x:Identifier,…) { x:Identifier = AssignmentExpression;… var y:Identifier = -NumericLiteral Identifier(-NumericLiteral),…… body:Statement…}
succeeds if:
imm (σ,…) → τ;
The ValidateStatement rule validates an asm.js statement. Each statement is validated in the context of a global environment Δ, a variable environment Γ, and an expected return type τ. Unless otherwise explicitly stated, a recursive validation of a subterm uses the same context as its containing term.
Validating a Block statement node
{ stmt:Statement… }
succeeds if ValidateStatement succeeds for each stmt.
Validating an ExpressionStatement node
;
succeeds if ValidateCall
succeeds for cexpr with actual return type void.
Validating an ExpressionStatement node
;
succeeds if ValidateExpression succeeds for expr with some type σ.
Validating an EmptyStatement node always succeeds.
Validating an IfStatement node
if ( expr:Expression ) stmt1:Statement else stmt2:Statement
succeeds
if ValidateExpression
succeeds for expr with a subtype of int
and ValidateStatement
succeeds for stmt1 and stmt2.
Validating an IfStatement node
if ( expr:Expression ) stmt:Statement
succeeds
if ValidateExpression
succeeds for expr with a subtype of int
and ValidateStatement
succeeds for stmt.
Validating a ReturnStatement node
return expr:Expression ;
succeeds if ValidateExpression succeeds for expr with a subtype of the expected return type τ.
Validating a ReturnStatement node
return ;
succeeds if the expected return type τ is void.
Validating an IterationStatement node
while ( expr:Expression ) stmt:Statement
succeeds
if ValidateExpression
succeeds for expr with a subtype of int
and ValidateStatement
succeeds for stmt.
Validating an IterationStatement node
do stmt:Statement while ( expr:Expression ) ;
succeeds
if ValidateStatement
succeeds for stmt
and ValidateExpression
succeeds for expr with a subtype of int.
Validate an IterationStatement node
for ( init:ExpressionNoInopt ; test:Expressionopt ; update:Expressionopt ) body:Statement
succeeds if:
int (if
present);
Validating a BreakStatement node
break Identifieropt ;
always succeeds.
Validating a ContinueStatement node
continue Identifieropt ;
always succeeds.
Validating a LabelledStatement node
: body:Statement
succeeds if ValidateStatement succeeds for body.
Validating a SwitchStatement node
switch ( test:Expression ) { case:CaseClause… default:DefaultClauseopt }
succeeds if
signed;
Cases in a switch block are validated in the context
of a global environment Δ, a variable
environment Γ, and an expected return type τ. Unless
otherwise explicitly stated, a recursive validation of a subterm uses
the same context as its containing term.
Validating a CaseClause node
case n:-NumericLiteral : stmt:Statement…
succeeds if
. character;
The default case in a switch block is validated in the
context of a global environment Δ, a variable
environment Γ, and an expected return type τ. Unless
otherwise explicitly stated, a recursive validation of a subterm uses
the same context as its containing term.
Validating a DefaultClause node
default : stmt:Statement…
succeeds if ValidateStatement succeeds for each stmt.
Each expression is validated in the context of a global environment Δ and a variable environment Γ, and validation produces the type of the expression as a result. Unless otherwise explicitly stated, a recursive validation of a subterm uses the same context as its containing term.
Validating an Expression node
, … , exprn:AssignmentExpression
succeeds with type τ if for every i < n, one of the following conditions holds:
void; or
and ValidateExpression succeeds for exprn with type τ.
Validating a NumericLiteral node
double if the source contains a . character; or
validates as type double;
fixnum if the source does not contain a . character and its numeric value is in the range [0, 231); or
unsigned if the source does not contain a . character and its numeric value is in the range [231, 232).
Note that the case of negative integer constants is handled under UnaryExpression.
Note that integer literals outside the range [0, 232) are invalid, i.e., fail to validate.
Validating an Identifier node
succeeds with type τ if Lookup(Δ, Γ, x) = τ.
Validating a CallExpression node succeeds with
type float
if ValidateFloatCoercion
succeeds.
Validating a MemberExpression node succeeds with type τ if ValidateHeapAccess succeeds with load type τ.
Validating an AssignmentExpression node
= expr:AssignmentExpression
succeeds with type τ if ValidateExpression succeeds for the nested AssignmentExpression with type τ and one of the following two conditions holds:
Validating an AssignmentExpression node
= rhs:AssignmentExpression
succeeds with type τ if ValidateExpression succeeds for rhs with type τ and ValidateHeapAccess succeeds for lhs with τ as one of its legal store types.
Validating a UnaryExpression node of the form
-NumericLiteral
succeeds with type signed if
the NumericLiteral source does not contain a .
character and the numeric value of the expression is in the range
[-231, 0).
Validating a UnaryExpression node of the form
+cexpr:CallExpression
succeeds with type double
if ValidateCall succeeds
for cexpr with actual return type double.
Validating a UnaryExpression node of the form
+-~!arg:UnaryExpression
succeeds with type τ if the type of op is … ∧ (σ) → τ ∧ … and ValidateExpression succeeds with a subtype of σ.
Validating a UnaryExpression node of the form
~~arg:UnaryExpression
succeeds with type signed
if ValidateExpression
succeeds for arg with a subtype of either double
or float?.
Validating a MultiplicativeExpression node
*/% rhs:UnaryExpression
succeeds with type τ if:
Validating a MultiplicativeExpression node
* n:-NumericLiteral-NumericLiteral * expr:UnaryExpression
succeeds with type intish if the source of n
does not contain a . character and -220
< n < 220
and ValidateExpressionexpr with a subtype of int.
Validating an AdditiveExpression node
+- … +- exprn
succeeds with type intish if:
int;
Otherwise, validating an AdditiveExpression node
+- rhs:MultiplicativeExpression
succeeds with type double if:
double;
Validating a ShiftExpression node
<<>>>>> rhs:AdditiveExpression
succeeds with type τ if
Validating a RelationalExpression node
<><=>= rhs:ShiftExpression
succeeds with type τ if
Validating an EqualityExpression node
==!= rhs:RelationalExpression
succeeds with type τ if
Validating a BitwiseANDExpression node
& rhs:EqualityExpressionsucceeds with type signed
if ValidateExpression
succeeds for lhs and rhs with
a subtype of intish.
Validating a BitwiseXORExpression node
^ rhs:BitwiseANDExpressionsucceeds with type signed
if ValidateExpression
succeeds for lhs and rhs with
a subtype of intish.
Validating a BitwiseORExpression node
|0succeeds with type signed
if ValidateCall succeeds
for cexpr with actual return type signed.
Validating a BitwiseORExpression node
| rhs:BitwiseXORExpressionsucceeds with type signed
if ValidateExpression
succeeds for lhs and rhs with
a subtype of intish.
Validating a ConditionalExpression node
? cons:AssignmentExpression : alt:AssignmentExpression
succeeds with type τ if:
int, double, or float;
int;
Validating a parenthesized expression node
( expr:Expression )
succeeds with type τ if ValidateExpression succeeds for expr with type τ.
Each function call expression is validated in the context of a global environment Δ and a variable environment Γ, and validates against an actual return type τ, which was provided from the context in which the function call appears. A recursive validation of a subterm uses the same context as its containing term.
Validating a CallExpression node
(arg:Expression,…)
with actual return type τ succeeds if one of the following conditions holds:
…)
→ τ ∧ …
and ValidateExpression
succeeds for the first n argi expressions
with subtypes of their corresponding σi and
the remaining arg expressions with subtypes of σ.
Alternatively, validating the CallExpression succeeds with
any actual return type τ other than float
if Lookup(Δ, Γ, f)
= Function
and ValidateExpression
succeeds for each arg with a subtype of extern.
Validating a CallExpression node
[index:Expression & n:-NumericLiteral](arg:Expression,…)
succeeds with actual return type τ if:
. character;
intish; and
Each heap access expression is validated in the context of a global
environment Δ and a variable environment Γ, and validation
produces a load type as well as a set of legal store
types as a result. These types are determined by
the heap view types corresponding to
each ArrayBufferView
type.
Validating a MemberExpression node
[n:-NumericLiteral]
succeeds with load type σ and store types { τ, … } if:
ArrayBufferView
type;
. character;
Validating a MemberExpression node
[expr:Expression >> n:-NumericLiteral]
succeeds with load type σ and store types { τ, … } if:
ArrayBufferView
type;
intish;
. character;
A call to the fround coercion is validated in the
context of a global environment Δ and a variable environment
Γ and validates as the type float.
Validating a CallExpression node
(cexpr:CallExpression)
succeeds with type float if Lookup(Δ,
Γ, f) = fround and ValidateCall succeeds for
cexpr with actual return type float.
Alternatively, validating a CallExpression node
(arg:Expression)
succeeds with type float if Lookup(Δ,
Γ, f) = fround
and ValidateExpression
succeeds for arg with type τ, where τ is a subtype
of floatish, double?, signed,
or unsigned.
An AOT implementation of asm.js must perform some internal dynamic checks at link time to be able to safely generate AOT-compiled exports. If any of the dynamic checks fails, the result of linking cannot be an AOT-compiled module. The dynamically checked invariants are:
return statement without throwing;
ArrayBuffer;
byteLength must be either 2n for n in [12, 24) or 224 · n for n ≥ 1;
If any of these conditions is not met, AOT compilation may produce invalid results so the engine should fall back to an interpreted or JIT-compiled implementation.
| Unary Operator | Type |
|---|---|
+ |
(signed) → double ∧( unsigned) → double ∧( double?) → double ∧( float?) → double
|
- |
(int) → intish ∧( double?) → double ∧( float?) → floatish
|
~ |
(intish) → signed |
! |
(int) → int |
Note that the special combined operator ~~ may be used
as a coercion from double or float?
to signed; see Unary
Expressions.
| Binary Operator | Type |
|---|---|
+ |
(double, double) → double ∧( float?, float?) → floatish
|
- |
(double?, double?) → double ∧( float?, float?) → floatish
|
* |
(double?, double?) → double ∧( float?, float?) → floatish
|
/ |
(signed, signed) → intish ∧( unsigned, unsigned) → intish ∧( double?, double?) → double ∧( float?, float?) → floatish
|
% |
(signed, signed) → intish ∧( unsigned, unsigned) → intish ∧( double?, double?) → double
|
|, &, ^, <<, >> |
(intish, intish) → signed |
>>> |
(intish, intish) → unsigned |
<, <=, >, >=, ==, != |
(signed, signed) → int ∧( unsigned, unsigned) → int ∧( double, double) → int ∧( float, float) → int
|
| Standard Library | Type |
|---|---|
InfinityNaN
|
double |
Math.acosMath.asinMath.atanMath.cosMath.sinMath.tanMath.expMath.log
|
(double?) → double |
Math.ceilMath.floorMath.sqrt
|
(double?) → double ∧( float?) → float
|
Math.abs |
(signed) → signed ∧( double?) → double ∧( float?) → float
|
Math.minMath.max
|
(int, int…) → signed ∧( double, double…) → double
|
Math.atan2Math.pow
|
(double?, double?) → double |
Math.imul |
(int, int) → signed |
Math.fround |
fround |
Math.EMath.LN10Math.LN2Math.LOG2EMath.LOG10EMath.PIMath.SQRT1_2Math.SQRT2 |
double |
| View Type | Element Size (Bytes) | Load Type | Store Types |
|---|---|---|---|
Uint8Array |
1 | intish |
intish |
Int8Array |
1 | intish |
intish |
Uint16Array |
2 | intish |
intish |
Int16Array |
2 | intish |
intish |
Uint32Array |
4 | intish |
intish |
Int32Array |
4 | intish |
intish |
Float32Array |
4 | float? |
floatish, double? |
Float64Array |
8 | double? |
float?, double? |
Thanks to Martin Best, Brendan Eich, Andrew McCreight, and Vlad Vukićević for feedback and encouragement.
Thanks to Benjamin Bouvier, Douglas Crosher, and Dan Gohman for
contributions to the design and implementation, particularly for
float.
Thanks to Jesse Ruderman and C. Scott Ananian for bug reports.
Thanks to Michael Bebenita for diagrams.